如何用程序画雪花

起因

在知乎看到一篇很有趣的帖子
用 C 语言画科赫雪花
作者利用递归的思想和相关的算法用以下字符画出了科赫雪花：

下划线(_)
减号(-)
斜杠(/)
反斜杠(\)
效果如下：

这种实现方法的好处是逻辑简单，易于实现。缺点是画出来的科赫雪花不够细致，因为毕竟是用ascii字符画出来的。
原理
基本思想上面的帖子已经阐述过了，这里引用以上帖子的两张图，如侵删。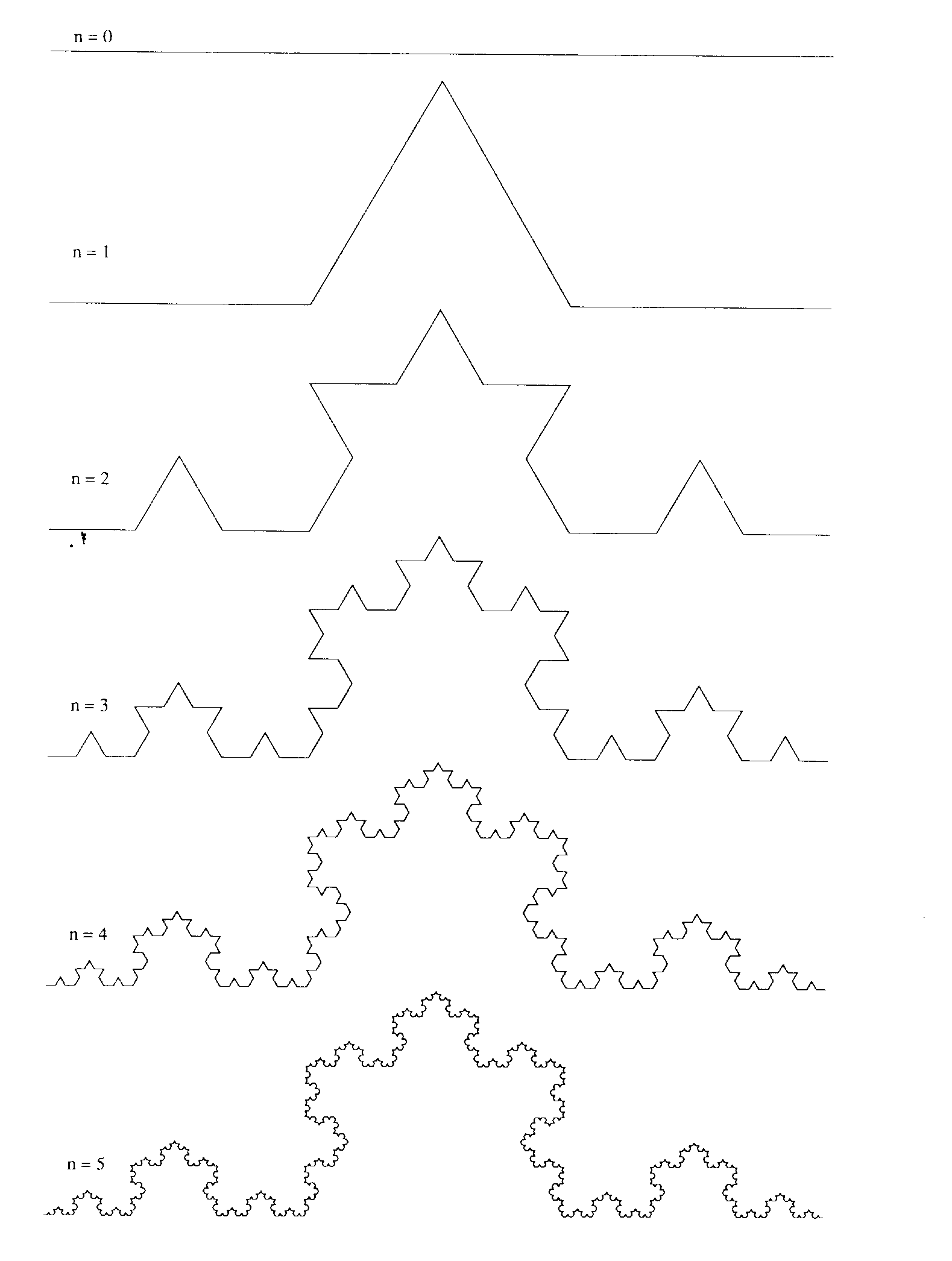

简单来说就是给定一条直线，分成三等分，选出中间的线段作等边三角形。如上图所视。不断地重复这个过程，即可画出科赫曲线。把三条科赫曲线组合在一起，便成了雪花形状，如下图所示：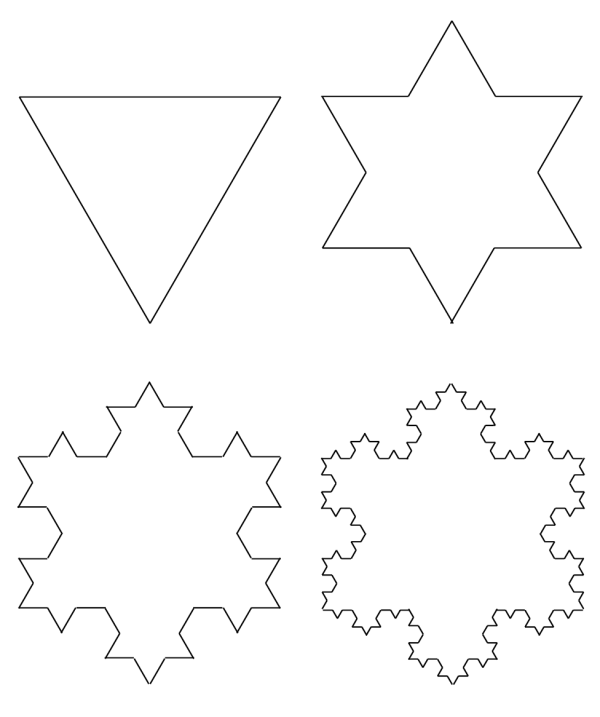

用字符画科赫雪花的方法刚才提到的帖子里面已经说了，下面讲画出精准的科赫雪花的方法。如下图所示：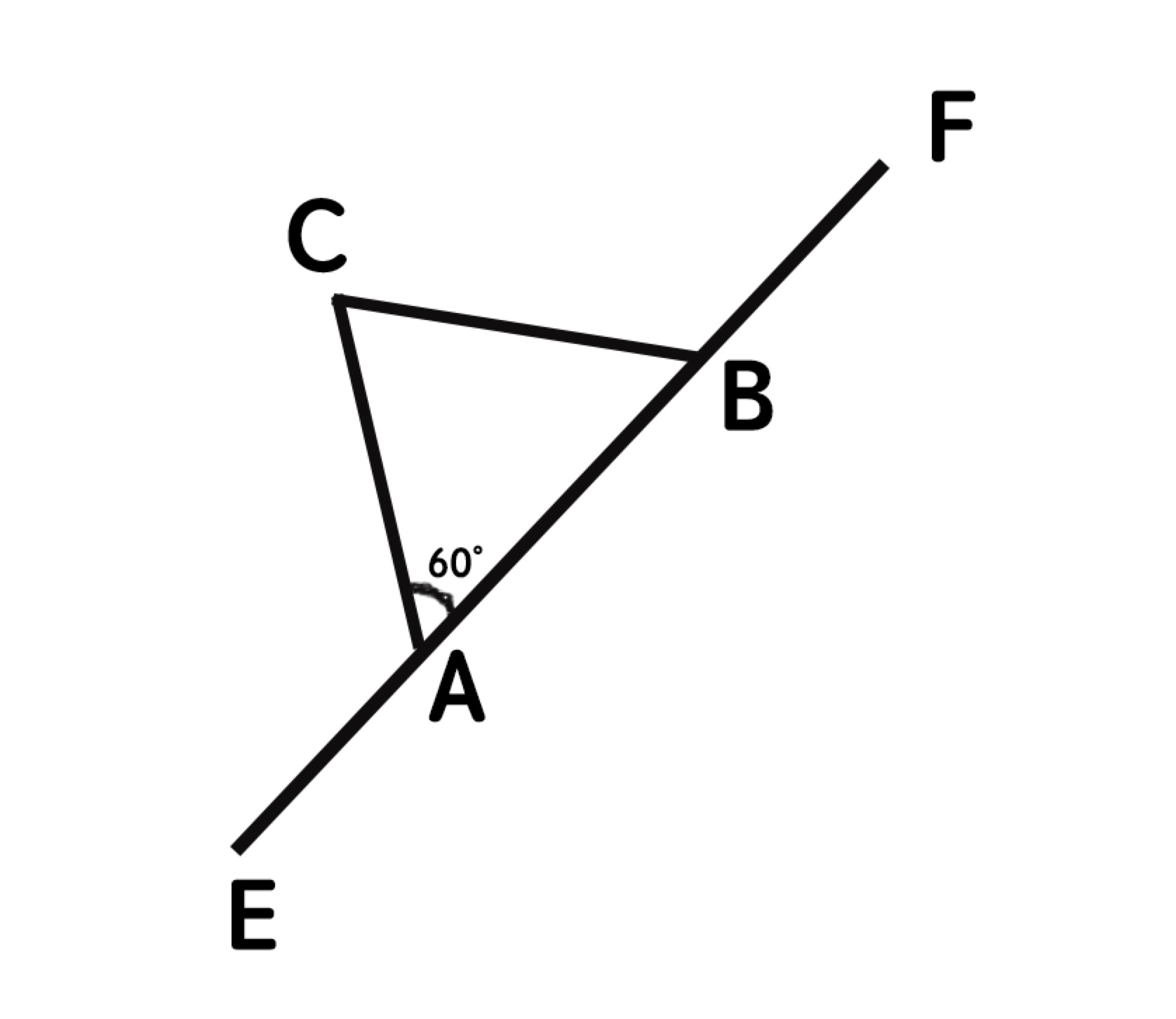

EF为原始线段，将其分成三等分，为EA、AB、BF,以AB为边作等边三角形ABC。开始的时候点E和点F已知，所以点A和点B的坐标很容易就可以求到。若E点和F点的坐标为：
E(x1, y1), F(x2, y2)
则
A(x1 * 2.0 / 3.0 + x2 * 1.0 / 3.0, y1 * 2.0 / 3.0 + y2 * 1.0 / 3.0)
B(x1 * 1.0 / 3.0 + x2 * 2.0 / 3.0, y1 * 1.0 / 3.0 + y2 * 2.0 / 3.0)
关键是点C的坐标比较难求。因为CA与BA的夹角为60° ，所以向量<A,C>可以看做是向量<A,B>逆时针旋转60° 的结果。我们复习一下旋转公式：
x = x0 * cosθ - y0 * sinθ
y = y0 * cosθ + x0 * sinθ
其中x0，y0是原始向量的横坐标和纵坐标，θ是逆时针旋转角，x、y是求出来的旋转后的向量的横坐标和纵坐标。
因为向量<A,B>很容易求出，而<A,C>是<A,B>逆时针旋转60°的结果，所以可以根据上面的旋转公式求出<A,C>，接着我们可以求出C点的坐标为：
C = A + <A,C>
至此，未知的A，B，C点都求出来了。接着，我们会把线段EA、AC、CB、BF作为原始线段，重复上面的过程，直到求出来的点足够多，足以拼成一个漂亮的雪花为止。
实现
大体思路
由于很多图形绘制引擎（比如OpenGL）绘制图像时候会先绘制一个个最基本的三角形，然后经过大量的三角形来组合成我们的图像。我们的工作是求出所有绘制雪花所需要的三角形上的点。例如，我们会首先绘制一个最基本的等边三角形。如图所示：

接着以等边三角形的边为基本边，按上诉步骤接着画三角形，如下图：

直到画出来的三角形足够多，图案看起来像雪花为止。

下面是代码实现：

Point结构体

无论是点还是向量都是由两个变量(x,y)组成的，我们定义一个简单的Point工具类：

struct Point {
    double x;
    double y;
    Point() {};
    Point(double x, double y) {
        this->x = x;
        this->y = y;
    }
    Point rotate(double angle) {
        Point result;
        result.x = x * cos(angle) - y * sin(angle);
        result.y = y * cos(angle) + x * sin(angle);
        
        return result;
    }
    Point operator +(Point p) {
        Point result;
        result.x = p.x + x;
        result.y = p.y + y;
        
        return result;
    }
    Point operator -(Point p) {
        Point result;
        result.x = x - p.x;
        result.y = y - p.y;
        
        return result;
    }
};

注意rotate是旋转函数，angle为指定的旋转角度，返回结果为旋转后的Point。

层次结构

我们定义一个类为KochCurve类，精简后的代码(省略了拷贝函数，析构函数等细节处理）如下：

class KochCurve {
public:
    KochCurve(Point p1, Point p2);
    void calc();
    Point* getPoints() {
        return pointToDraw;
    }
    KochCurve** getKochCurves() {
        return kcs;
    }
private:
    Point point[2];
    Point pointToDraw[3];
    KochCurve *kcs[4];
};
//初始化
KochCurve::KochCurve(Point p1, Point p2) {
    point[0] = p1;
    point[1] = p2;
    
    int i;
    for(i = 0; i < 4; i++) {
        kcs[i] = NULL;
    }
    
}
//计算函数，计算用于画三角形的A、B、C点，以及EA，AC，CB，BF这四条边，它们将会作为下一个计算回合的基本边
void KochCurve::calc() {
    pointToDraw[0].x = 2.0 / 3 * point[0].x + 1.0 / 3 * point[1].x;
    pointToDraw[0].y = 2.0 / 3 * point[0].y + 1.0 / 3 * point[1].y;
    
    pointToDraw[1].x = 1.0 / 3 * point[0].x + 2.0 / 3 * point[1].x;
    pointToDraw[1].y = 1.0 / 3 * point[0].y + 2.0 / 3 * point[1].y;
    
    
    pointToDraw[2] = pointToDraw[0] + (pointToDraw[1] - pointToDraw[0]).rotate(PI / 3);
    
    kcs[0] = new KochCurve(point[0], pointToDraw[0]);
    kcs[1] = new KochCurve(pointToDraw[0], pointToDraw[2]);
    kcs[2] = new KochCurve(pointToDraw[2], pointToDraw[1]);
    kcs[3] = new KochCurve(pointToDraw[1], point[1]);
}

该类主要是以下结构：

类成员与上图的对应关系为：

数组point[2]为基本线两个端点E和F，其中point[0]为E，point[1]为F
数组pointToDraw[3]主要指用来绘制三角形的点，它们是A，B，C。其中，pointToDraw[0]表示A点，pointToDraw[1]表示B点，pointToDraw[2]表示C点。

kcs的意思是（KochCurves），数组kcs的长度为4个，表示四条线段EA、AC、CB、BF，它们将会作为下一个计算回合的基本边。

##### 雪花类
直接上代码，结合代码看下面的注解：
``` c++
class SnowFlake {
public:
    SnowFlake(Point p1, Point p2, Point p3, int depth);
    void calc();
    int getLen() {
        return len;
    }
    Point* getPoints() {
        return points;
    }
private:
    int depth;
    int len;
    KochCurve kc[3];
    
    int index;
    Point *points;
    
    
    void createPoints(KochCurve *kc, int d);
};
SnowFlake::SnowFlake(Point p1, Point p2, Point p3, int depth) {
    kc[0] = KochCurve(p1, p2);
    kc[1] = KochCurve(p2, p3);
    kc[2] = KochCurve(p3, p1);
    
    this->depth = depth;
    index = 0;
    
    
    len = 3 + 3 * (pow(4, depth) - 1);
    points = new Point[len];
    
    
    points[index++] = p1;
    points[index++] = p2;
    points[index++] = p3;
}
void SnowFlake::calc() {
    int i;
    for(i = 0; i < 3; i++) {
        createPoints(&kc[i], depth);
    }
    
    cout<<"index:"<<index<<endl;
    cout<<"len:"<<len<<endl;
    
}
void SnowFlake::createPoints(KochCurve *kc, int d) {
    if(d == 0)
        return;
    kc->calc();
    Point *ps = kc->getPoints();
    int j;
    for(j = 0; j < 3; j++) {
        points[index++] = ps[j];
    }
    KochCurve **kcs = kc->getKochCurves();
    int i;
    for(i = 0; i < 4; i++) {
        createPoints(kcs[i], d - 1);
    }
}

雪花类的构造函数接受4个参数，前三个为基本三角形的三个点，一般我们会传入一个等边三角形的三个点，最后一个参数是depth（深度），这个参数指定程序会将上诉的流程（“原理”一节中的流程，也就是把一条基本线平均分成3份，在中间份的基础上做等边三角形）递归地执行多少次。那么，当深度为depth时候，我们需要一个多大的空间来存储点呢？我们计算一下当深度为depth的时候会生成多少个点。
首先开始的时候我们需要花一个等边三角形，生成了3个点。接着以等边三角形的每一条边为基本线，开始以当前计算回合的A点B点C点为顶点画三角形。所以总的点数为：
point num = 3 + 3 * (3 + 3 * 4 + 3 * 4 * 4 + … + 3 * 4 ^ (depth - 1)) = 3 + 3 * (4 ^ depth - 1)
雪花类的成员变量以及成员函数注解如下：

depth为计算深度，递归次数
len为点数，即上面计算出来的point num
数组kc[3]为三条科赫曲线。
index为points数组的当前写索引
计算出来的所有点会被存于points数组中

调用示例

如果你看了上面还没明白，看看下面的调用示例：

//生成雪花对象，指定基础等边三角形的顶点和计算深度
SnowFlake sf(Point(-0.5, 0.5), Point(0.5, 0.5), Point(0.0, -0.36602), 5);
//计算所有的点
   sf.calc();
   //获取计算出来的所有的点
   Point *points = sf.getPoints();
   //获取长度
   int i, len = sf.getLen();
   //2d坐标转换成OpenGL的3D坐标（指定z坐标为0）
   for(i = 0; i < len; i++) {
       vertices.push_back((GLfloat)points[i].x);
       vertices.push_back((GLfloat)points[i].y);
       vertices.push_back(0.0f);
   }
   //画三角形
   ...

最后的实现效果：

后续优化

如果指定初始等边三角形的点，则雪花的全部坐标就已经定下来了，所以我们没必要在运行时对其进行运算，我们可以在程序开始运行之前把相应的点给计算出来。一种解决方案是编写一个小程序把雪花坐标给全部计算出来，然后把它们存储在一个文件中，这样画雪花的程序在开始画雪花之前只需要把坐标数据读入就好了。另一种解决方案是利用c++的模板元递归技术。在编译时候就把雪花所有坐标给计算好，在运行的时候直接取值就好了。

作者水平有限，难免有错误的地方，欢迎指正。
代码经调整后稍后奉上。

起因

原理

实现

大体思路

Point结构体

层次结构

调用示例

后续优化