Jinlong's Blog

快速幂运算算法

发表于

一般思路的求幂函数会是如下所示：

1
2
3
4
5
6
7
long long power(int a, int n) {
	int i;
	long long result = 1;
	for(i = 0; i < n; i++)
		result *= a;
	return result;
}

以上函数算法复杂度为O(n)，快速幂算法可以将幂运算的算法复杂度降到O(logn)。原理如下。
比如计算3^13，因为13的二进制表示为1101，所以：

1
3 ^ 13 = 3 ^ [1] * 3 ^ [00] * 3 ^ [100] * 3 ^ [1000]

（注：中括号内为二进制表示）
类似的，我们对于所有幂运算都可以化成以上形式，算法复杂度由原来的O(n)变为O(logn)，矩阵快速幂运算代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//重载矩阵类的^运算符
Matrix operator^(int n) {
	Matrix result, multi;
	result.init();   //初始化为单位矩阵
	multi = *this;	 
	while(n) {
		if(n & 0x1) {
			result = result * multi;
		}
		multi = multi * multi;
		n >>= 1;
	}
	return result;
}

(注：Matrix为矩阵)

应用（快速计算斐波那契数列）：
一般计算斐波那契数列我们用递推的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
long long calc1(int n) {
	if(n == 1 || n == 2)
		return 1;
	else if(n <= 0)
		return -1;
	int i;
	long long *arr = new long long[n];
	arr[0] = 1;
	arr[1] = 1;
	for(i = 2; i < n; i++) {
		arr[i] = arr[i - 1] + arr[i - 2];
	}
	return arr[i - 1];
}

如果我们要求斐波那契数列的第一亿项，递推求值的方式将会花费很长的时间。
由于f(n) = f(n - 1) + f(n - 2)，所以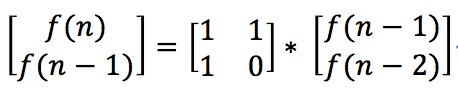
quick2.jpg
推出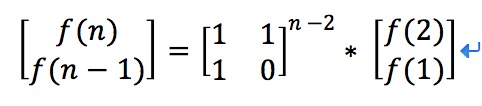
quick1.jpg
至此我们就可以在求斐波那契数列中应用上快速幂运算了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
long long calc2(int n) {
	if(n == 1 || n == 2)
		return 1;
	else if(n <= 0)
		return -1;
	Matrix m;
	m.arr[0][0] = 1;
	m.arr[0][1] = 1;
	m.arr[1][0] = 1;
	m.arr[1][1] = 0;
	Matrix a = m ^ (n - 2);
	return a.arr[0][0] * 1 + a.arr[0][1] * 1;
}