哈希树笔记

结构

哈希树的结构如下图所示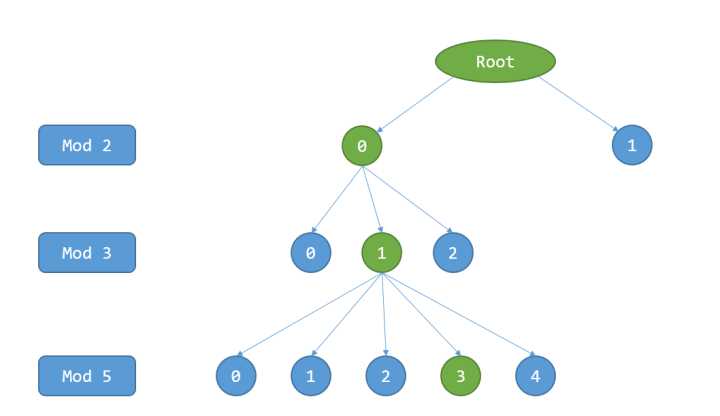

主要思想是：插入的每一个数据通过模多个质数来确定在树中的位置。图为四层哈希树，除第一层外每一层都会有一个质数对即将插入的数取模，质数从最小开始，逐步增大，如图中第二层的质数为2，第三层为3，第四层为5（如果有第五层则为7）。首先假设最下面一层（第四层）才存储数据，其它层（第一道三层）都不存储数据。假如要插入28，则其检索路径就如上图所示。最终它被插入到第四层的绿色节点中。

容量

基于哈希树最下面一层才存储数据的假设，一个4层哈希树的存储容量为
2 * 3 * 5 = 30

容量内不会发生冲突

哈希数据结构最主要的问题是解决键值的冲突。神奇的是，哈希树在容量范围内并不会发生冲突，比如上图的四层哈希树的键值在30以内并不会发生冲突。一个8层的哈希树的容量为：
2 * 3 * 5 * 7 * 11 * 13 * 17 = 510510
且键值在510510内不会发生冲突。
证明如下：

要证明哈希树在容量范围内并不会发生冲突，只需要证明树中存储数据的任意一个节点只对应容量范围内的唯一一个数即可。
设现有一颗n + 1层的哈希树，从第二层到第n+1层的质数分别为m₁,m₂,m₃…m_n。现有一个容量范围内的数据x，x除以m₁的余数为a₁，除以m₂的余数为a₂，以此类推。即：
x ≡ a₁ (mod m₁)
x ≡ a₂ (mod m₂)
x ≡ a₃ (mod m₃)
…
x ≡ a_n (mod m_n)
令
t₁ = k₁m₁ + a₁(k₁为非负整数，下面同上)
t₂ = k₂m₂ + a₂
…
t_n = k_nm_n + a_n
下面我们试着构造T = t₁ + t₂ + … + t_n，使得T满足：
T ≡ a₁ (mod m₁)
T ≡ a₂ (mod m₂)
T ≡ a₃ (mod m₃)
…
T ≡ a_n (mod m_n)
我们知道，如果t₁ % m₁ = a₁，则(t₁ + km₁) % m₁ = a₁，所以若要(t₁ + t₂) % m₁ = a₁，则需t₂为m₁的倍数，以此类推，若要(t₁ + t₂ + … + t_n) % m₁ = a₁，则当t₂,t₃…t_n都为m₁的倍数的时候,等式成立。所以若要：
T % m₁ = a₁
T % m₂ = a₂
…
T % m_n = a_n
则：
t₁除以m₁余a₁，t₂,t₃ … t_n都是m₁的倍数
t₂除以m₂余a₂，t₁,t₃ … t_n都是m₂的倍数
…
t_n除以m_n余a_n，t₁,t₂ … t_{n - 1}都是m_n的倍数
整理得：
t₁除以m₁余a₁，t₁是m₂,m₃…m_n的公倍数
t₂除以m₂余a₂，t₂是m₁,m₃…m_n的公倍数
…
t_n除以m_n余a_n，t_n是m₁,m₂…m_{n - 1}的公倍数
置：
t₁为满足 除以m₁余a₁且为(m₂m₃…m_n)的倍数 的数
t₂为满足 除以m₂余a₂且为(m₁m₃…m_n)的倍数 的数
…
t_n为满足 除以m_n余a_n且为(m₁m₂…m_{n - 1})的倍数 的数
即：
t_i = a_iM_iM_i^-1
（其中M = m₁ + m₂ + … + m_i, M_i = M / m_i, M_i^-1为M_i的逆元）
此时T = t₁ + t₂ + … + t_n满足：
T % m₁ = a₁
T % m₂ = a₂
…
T % m_n = a_n
但此时的T不是最小解。若a % b = c，则（a - kb) % b = c，所以
x = T - kM（k尽量大，只要x不为负即可）
所以x = T % M，即:
x = (a₁M₁M₁^-1 + a₂M₂M₂^-1 + … + a_nM_nM_n^-1) % (m₁m₂…m_n)
所以x是一个小于容量M的唯一的整数解，所以哈希树最后一层的每个位置都可以对应一个容量内的唯一一个整数，所以哈希树在容量内不会发生冲突。

变体

以上所述的哈希树只是在最后一层可以存储数据，容量为：
m₁m₂…m_n
事实上，为了节省空间，第二层到最后一层都可以存储数据，下面这张图很好地说明了这一点：

变体的容量为：
m₁ + m₁m₂ + m₁m₂m₃ + … + m₁m₂…m_n

与哈希表比较

哈希树与哈希表的能实现的功能基本一样，但与哈希表不同的是，哈希树算法是稳定算法，查询一个数据的算法复杂度是O(k)，而哈希表查询一个数据正常情况下是O(1)。而且当需要更多的空间存储数据的时候，哈希树只需要增加层数即可，而哈希表需要更多的空间存储数据时则需要rehash并对空间扩容，相对比较麻烦。